[백준] 14500 테트로미노

문제 설명

폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다.

• 정사각형은 서로 겹치면 안 된다.
• 도형은 모두 연결되어 있어야 한다.
• 정사각형의 변끼리 연결되어 있어야 한다. 즉, 꼭짓점과 꼭짓점만 맞닿아 있으면 안 된다.

정사각형 4개를 이어 붙인 폴리오미노는 테트로미노라고 하며, 다음과 같은 5가지가 있다.

 

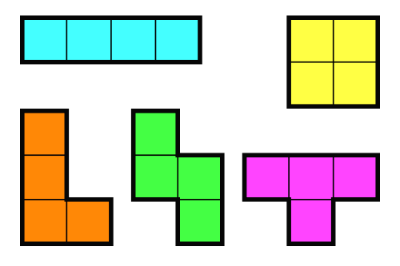
아름이는 크기가 N×M인 종이 위에 테트로미노 하나를 놓으려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 정수가 하나 쓰여 있다.

테트로미노 하나를 적절히 놓아서 테트로미노가 놓인 칸에 쓰여 있는 수들의 합을 최대로 하는 프로그램을 작성하시오.

테트로미노는 반드시 한 정사각형이 정확히 하나의 칸을 포함하도록 놓아야 하며, 회전이나 대칭을 시켜도 된다.

 

입력

• 첫째 줄에 종이의 세로 크기 N과 가로 크기 M이 주어진다. (4 ≤ N, M ≤ 500)
• 둘째 줄부터 N개의 줄에 종이에 쓰여 있는 수가 주어진다. i번째 줄의 j번째 수는 위에서부터 i번째 칸, 왼쪽에서부터 j번째 칸에 쓰여 있는 수이다. 입력으로 주어지는 수는 1,000을 넘지 않는 자연수이다.

 

입력 예

5 5
1 2 3 4 5
5 4 3 2 1
2 3 4 5 6
6 5 4 3 2
1 2 1 2 1

 

출력

• 첫째 줄에 테트로미노가 놓인 칸에 쓰인 수들의 합의 최댓값을 출력한다.

 

 

출력 예

19

 

풀이

#include <iostream>
#include <algorithm>
#define MAX_SIZE 500
using namespace std;

int N, M, MAX = 0;
int map[MAX_SIZE][MAX_SIZE] = {0, };
bool visited[MAX_SIZE][MAX_SIZE] = {0, };

// 동 서 북 남
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};

bool inRange(int x, int y) {
    if (x < 0 || x >= N || y < 0  || y >= M)
        return false;
    else
        return true;
}

// 'ㅗ', 'ㅏ', 'ㅓ', 'ㅜ' 를 제외한 모든 모양에 해당되는 dfs 함수
void move(int x, int y, int count, int sum) {
    
    // 조각 4개가 모였다면 max 업뎃
    if (count == 4) {
        MAX = max(MAX, sum);
        return;
    }

    // 동 서 남 북 dfs
    for (int i = 0; i < 4; i++) {
        int nx = x + dx[i];
        int ny = y + dy[i];

        if (inRange(nx, ny) && !visited[nx][ny]) {
            visited[nx][ny] = 1;
            move(nx, ny, count+1,  sum + map[nx][ny]);
            visited[nx][ny] = 0;
        }
    }
}

// 'ㅗ', 'ㅏ', 'ㅓ', 'ㅜ' 에 해당되는 dfs로 처리 불가한 모양
void specialShape(int x, int y) {
    for (int i = 0; i < 4; i++){
        int sum = map[x][y];
        bool flag = true;
        
        // 중심을 제외하고 상, 하, 좌, 우 중 3개 
        for (int j = 0; j < 3; j++) {
            int nx = x + dx[(i+j) % 4];
            int ny = y + dy[(i+j) % 4];

            if (inRange(nx, ny)) {
                sum += map[nx][ny];
            }
            else {
                flag = false;
                break;
            }
        }

        if (flag) {
            MAX = max(MAX, sum);
        }
    }
}

int main () {
    ios_base::sync_with_stdio(false);
    cin.tie(0);

    cin >> N >> M;

    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++) {
            cin >> map[i][j];
        }
    }

    for (int i = 0; i < N*M; i++) {
        int x = i / M; // 행
        int y = i % M; // 열

        visited[x][y] = 1;

        move(x, y, 1, map[x][y]); // dfs start
        specialShape(x, y); // specialShape start

        visited[x][y] = 0; // dfs 후 visit[][] 0 처리
    }

    cout << MAX << endl;

    return 0;
}

 

리뷰

• 난이도가 있는 DFS 문제이다.
• 'ㅗ', 'ㅜ', 'ㅏ', 'ㅓ' 모양은 DFS로 구할 수 없다는 것이 함정이다.
• 해당 블록의 경우 specialShape로 따로 구하였다.
• 자기 자신(가운데) 블록에 상, 하, 좌, 우 중 3 방향의 블록을 번갈아 가며 붙여 4가지의 블록을 만든다.
• DFS가 끝난 후마다 꼭 'visit[][]  0처리'를 해줘야 한다. => 다른 모양으로 해당 자리에 올 수 있기 때문
• 4가지의 블록이 모였다면 하나의 모양이 완성 된 것이다. 따라서, Max값 업데이트를 해준다.
• 좋은 풀이가 있어서 참고하였다.

 

해당 문제 링크

https://www.acmicpc.net/problem/14500

14500번: 테트로미노